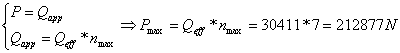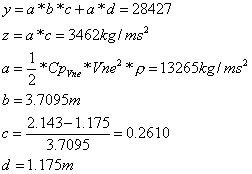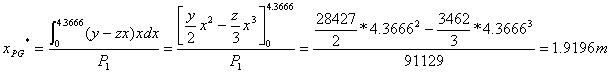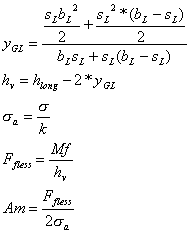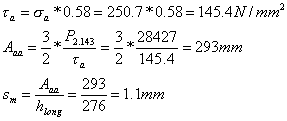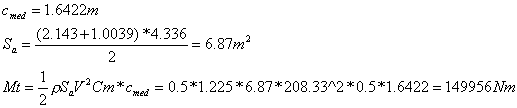Carichi agenti sull’ala

            L’ala, costituita dall’insieme delle due semiali, rappresenta l’elemento portante di un aeroplano; ciò sta a significare che questa struttura deve essere in grado di sviluppare la portanza necessaria al volo del velivolo. Ricordando la [f.01], è possibile affermare che, fissati i valori di quota (che è sinonimo di densità, nell’ipotesi che il volo avvenga in aria calma e con le stesse caratteristiche dell’aria tipo), velocità e Cp, il valore della portanza dipenderà solamente dalla superficie alare di cui il velivolo dispone. Quindi, maggiore è la superficie, e maggiore è la portanza che un dato aeromobile è in grado di sviluppare. Una superficie alare molto estesa, però, implica l’impiego di un’ala moto grande, e cioè di un peso considerevole.

Anche le dimensioni dell’ala, quindi, sono da tenere in grande considerazione. Molta rilevanza assume anche la forma dell’ala: diverse forme della pianta alare danno origine a diverse distribuzioni della portanza, creando, magari, degli effetti indesiderati. Una notevole importanza riveste lo studio della distribuzione dei carichi e, soprattutto, della portanza lungo l’apertura alare.

L’ala vista come mensola o trave a sbalzo

            Prendendo in considerazione una semiala del velivolo Bf. 109, si nota che questa è di tipo monolongherone con struttura ad anima sottile. Il longherone, posto al 40% di ogni centina, costituisce la parte strutturalmente più importante di tutta la semiala, ad un’estremità del quale sono posti gli appositi agganci che costituiranno il punto di unione tra la semiala ed il velivolo.

È facile immaginare, quindi, una semiala come una trave a sbalzo, cioè una trave vincolata ad un’estremità e sulla quale gravano dei carichi. Generalmente, su di un ala (o semiala) agiscono due tipo di carichi: quelli dovuti a fattori di tipo aerodinamico e quelli dovuti al peso dell’ala stessa. In particolare, i due principali carichi dovuti a fattori di tipo aerodinamico sono la portanza ed il momento torcente.

La portanza e la sua distribuzione

            Fino a questo momento si è parlato di portanza come di una forza unica, applicata al baricentro del velivolo. Questa visione, comunque, non è del tutto veritiera, in quanto, la portanza totale di un velivolo, che fino ad ora è stata chiamata per semplicità portanza, è data dalla sommatoria di diverse forze.

Come si è potuto osservare, una volta impostati i dati relativi al profilo impiegato, alla quota ed alla velocità di volo, la portanza dipende solamente dall’entità della superficie portante di un aereo. Anche se in minima parte, anche la fusoliera stessa è portante, come sono portanti i piani di coda ed altre superfici disposte sul velivolo, ma a causa dell’esiguità della forza sostentatrice da esse creata si considererà come unica superficie portante l’ala.

            La forma in pianta dell’ala assume una certa rilevanza nella progettazione delle strutture resistenti, in quanto, una modificazione della forma alare comporta una variazione nella distribuzione della portanza lungo l’apertura alare. Infatti, la portanza che si genera sull’ala è la risultante di tutta una serie di piccole forze sostentatrici, il cui modulo ed il cui punto di applicazione variano a seconda della dimensione della corda alare.

Per ricollegarsi alla descrizione dell’ala fatta in precedenza, se si considera questa struttura come formata da una serie infinita di profili alari posti l’uno vicino all’altro ed uniti attraverso una copertura, è facile immaginare come ognuno di questi profili generi una propria portanza, e che la portanza totale generata dall’ala non sia altro che la sommatoria di tutte le portanze proprie dei vari profili. Infatti, prendendo in considerazione un determinato profilo dotato di spessore infinitesimo, la superficie portante che questo possiede dipende esclusivamente dalla sua corda, e la portanza di tale profilo sarà data dal prodotto tra la corda del profilo ed i fattori già descritti, secondo la formula

  [f.08]

nella quale con “c” è indicato il valore della corda alare e con “s” lo spessore del profilo, il quale, essendo infinitesimo, diviene trascurabile, dando origine all’ultima parte dell’uguaglianza riportata.

Prima di passare alla determinazione della distribuzione della portanza sull’ala del Bf. 109, è opportuno spiegare quale potrebbe essere la distribuzione migliori dei carichi lungo l’apertura alare: più la distanza tra il vincolo ed il punto di applicazioni dei carichi agenti è maggiore, e più aumenta il momento flettente che questi carichi generano, facendo così aumentare la sezione resistente di vincolo.

Applicando un carico concentrato su di una semiala, quindi, la struttura resistente posta nella sezione di vincolo del longherone dovrà far fronte ad un momento flettente massimo quando il punto di applicazione del carico concentrato corrisponderà con l’estremo non vincolato della trave, mentre mano a mano che questo punto di applicazione si sposta verso la sezione di vincolo il braccio del momento flettente diminuisce, facendo diminuire anche lo stesso momento flettente.

Sarebbe opportuno quindi che i carichi agenti su di una semiala trovassero i loro punti di applicazione nella parte vicina alla sezione di radice, in modo da far diminuire l’intensità del momento flettente che essi creano.

Considerando quanto detto in precedenza a proposito della formazione della portanza lungo l’apertura alare, se ne deduce che, in una situazione il più possibile ottimale, la portanza generata dai profili posti verso l’estremità alare dovrà essere minore di quella generata dai profili posizionati vicino alla sezione di radice, facendo così spostare il punto di applicazione della portanza totale di una semiala verso la sezione vincolata, in modo da diminuire l’entità del momento flettente.

Per fare questo, è possibile agire in due diversi modi: ricordando che la portanza relativa ad un singolo profilo varia secondo la formula

                  [f.09]

stabiliti la quota e la velocità di volo, cioè i due parametri costanti per qualsiasi parte del velivolo, restano da poter modificare i valori relativi a Cp ed alla c.

Modificare il valore del coefficiente di portanza potrebbe voler dire due cose: cambiare tipo di profilo per le zone di estremità oppure modificare l’incidenza di questi profili lasciandone inalterata la forma. In particolare, questa seconda possibilità, darebbe origine ad un’ala “svergolata”, dotata, cioè, di profili con diverso angolo di incidenza.

La soluzione più semplice per diminuire la portanza nelle zone di estremità resta comunque quella di diminuire la corda alare mano a mano che il profilo assume una distanza maggiore dalla sezione di radice. Questa soluzione porta alla creazione di un’ala “rastremata”, caratterizzata da una corda alla radice maggiore di quella posta all’estremità alare.

Con un’ala rastremata, la soluzione ottimale per la distribuzione della portanza sarebbe quella di avere una corda all’estremità minima, possibilmente nulla. Per questa ragione è stata creata l’ala elittica, dotata di una distribuzione della portanza che varia elitticamente raggiungendo il massimo nella sezione di radice e diminuendo gradatamente fino a raggiungere un valore nullo in prossimità dell’estremità alare.

            Anche se il Bf. 109 non è dotato di un’ala a pianta elittica, la rastremazione dovuta alla sua ala di forma trapezia consente di ottenere una distribuzione di portanza molto vicina a quella elittica, ottimizzando la ripartizione degli sforzi lungo l’apertura alare. L’estremità arrotondata della sua ala, inoltre, oltre a diminuire i vortici marginali contribuisce a migliorare la distribuzione della portanza.

Distribuzione della portanza sul velivolo Bf. 109

            Prendendo in considerazione, per semplicità, una sola semiala di questo velivolo, si potrà notare che la lunghezza del longherone in essa montato non è sufficiente a farlo congiungere con quello montato sull’altra semiala, come avviene in molti modelli di aeroplani, e che non è neanche sufficiente a coprire tutta la semi-apertura alare del velivolo. Infatti, il longherone di ogni semiala si collega direttamente alla fusoliera attraverso appositi perni, e la sua lunghezza è stata studiata in modo da essere sufficiente a sopportare determinati carichi e momenti flettenti: a causa della rastremazione, infatti, la parte più esterna della semiala non fornisce una portanza notevole, o comunque, così grande da giustificare la presenza di un longherone. Questo risparmio in termini di lunghezza equivale ad un risparmio anche in termini di peso, il quale non può comportare altro che un vantaggio per le prestazioni del velivolo.

Considerando ora lo schema relativo alla disposizione del longherone all’interno della semiala sinistra presentato, si andrà a determinare analiticamente la distribuzione della portanza lungo tutta la semi-apertura alare.

Condizioni di calcolo

Prima di eseguire un qualsiasi calcolo relativo alla distribuzione della portanza in base alla corda alare, è necessario individuare con precisione il valore dei fattori da cui la portanza dipende, ed in particolare di Cp e V. Naturalmente, come già specificato, si considererà il velivolo mentre volo a quota zero, in modo da far assumere alla densità il suo valore massimo, considerando come termini di paragone i valori della densità a quote superiori a questa. Come prescritto dalle tabelle dell’aria tipo, quindi, il valore della densità s.l.m. è paria a 1.225 kg/m³.

Per ottenere le condizioni di volo più sfavorevoli per il velivolo, cioè quelle per cui l’aereo viene progettato, si andrà ad impostare un volo alla massima velocità ed al massimo fattore di carico, nonché con un peso pari a quello massimo di decollo. Con queste condizioni si procede alla determinazione della portanza necessaria per un volo in equilibrio: dalle considerazioni esposte durante questa trattazione si deduce che:

dove con Q_app viene indicato il peso apparente del velivolo durante una manovra, e con Q_eff il peso massimo al decollo.

Determinata la portanza massima, in base ai dati in possesso e,  ricordando che la superficie alare nominale di questo velivolo è pari a 16.03m², si determina il Cp, il cui valore che verrà poi utilizzato per la determinazione della portanza dei singoli profili costituenti l’ala. Ricordando la [f.01], si ricava il Cp desiderato:

Calcolo analitico della distribuzione della portanza

            Considerando lo schema dell’ala sinistra del velivolo Bf. 109 presentato, si può notare che la centina n°01 è la prima vera centina della semiala, in quanto, nella parte che va da questa centina agli attacchi longherone-fusoliera, il profilo della semiala è notevolmente condizionato dalla superficie di raccordo ala-fusoliera, la quale assume un profilo simile a quello utilizzato per la costruzione delle centine ma non del tutto identico. Per questo motivo, è possibile determinare con precisione la distribuzione della portanza solo dalla prima alla tredicesima centina, oltre la quale, come verrà dimostrato in seguito, sarà necessario avvalersi di un sistema approssimato.

Ricordando la [f.09], la portanza generata dal profilo della centina 01 sarà:

Il profilo della centina n°13 creerà una portanza paria a

Tra queste due centine, la portanza diminuisce linearmente, come del resto diminuisce linearmente anche il valore della corda del profilo mano a mano che ci si allontana dalla sezione di radice. Su questa parte di semiala, quindi, agirà un carico trapezio, i cui valori massimo e minimo saranno quelli della portanza calcolata rispettivamente nelle sezioni riguardanti le centine 01 e 13.

Per avere una conferma di tipo matematico di questa affermazioni, non basterà fare altro che determinare la formula del decremento del valore della corda al variare della distanza della sezione considerata da quella di radice, e sostituire il valore così ottenuto nella [f.09].

Operando matematicamente, si ottiene la formula

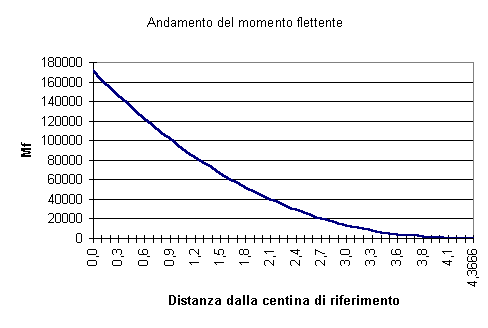
         [f.10]

dove con “P_x” viene indicata il valore assunto dalla portanza in una determinata sezione distante “x” dalla sezione di riferimento, cioè dalla centina 01. Gli altri valori assumono i seguenti valori:

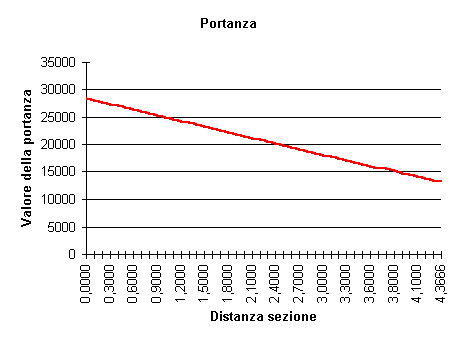
            Come si potrà sicuramente notare, nelle formule qui descritte vi è un errore relativo alle unità di misura: questo errore deriva dal fatto che, per semplicità, durante i calcoli non è stato inserito il parametro “dp”, relativo allo spessore infinitesimo del profilo considerato. Questo fatto è dovuto alla volontà di evitare di addentrarsi nella risoluzioni di particolari equazioni parametriche, dalle quali non si sarebbe potuto ottenere il risultato desiderato. Per quanto riguarda il parametro “dp”, comunque, esso assume un valore pari ad uno, e per questa ragione che la sua assenza non influisce minimamente sui risultati numerici ottenuti dall’utilizzo delle formule appena descritte. Fatto presente questo fatto, sarà quindi possibili utilizzare le formule riportate senza ulteriori problemi, in quanto, se il parametro “dp” venisse inserito, la verifica relativa alle unità di misura darebbe esito positivo.

            Dall’applicazione della [f.10], si ottiene il seguente diagramma relativo alla distribuzione della portanza lungo tutto il longherone:

 Per la parte relativa all’estremità alare, invece, le cose si rivelano un po’ più complesse: essendo l’estremità stessa arrotondata, e non avendo a disposizione dati certi relativi ai raggi dei raccordi utilizzati, il problema della distribuzione della portanza viene risolto con un metodo approssimativo. L’errore dovuto a questo metodo, comunque, non creerà alcun problema per la struttura, in quanto i dati così ottenuti non faranno altro che creare un leggero sovradimensionamento del longherone a favore della sicurezza.

Basandosi sull’ipotesi che l’estremità alare non sia arrotondata, ma che, invece, assuma la forma trapezia caratterizzante la semiala, si creerà un prolungamento naturale del trapezio principale esistente tra le centine 01 e 13. Questa nuova forma relativa all’estremità alare comporterà la formazione di un momento flettente teorico maggiore di quello reale, dando origine quindi ad un sovradimensionamento della struttura. Tale modificazione garantirà una maggiore sicurezza durante il volo.

Procedendo nei calcoli, per determinare la distribuzione della portanza in questa parte di ala ci si rifarà al metodo precedentemente utilizzato tra le centine 01 e 13: calcolando quindi la portanza nella sezione relativa alla 13^ centina ed in quella virtuale di estremità, si otterranno i valori massimo e minimo della portanza in questa parte di ala.

            Andando a rappresentare in un grafico la distribuzione della portanza lungo una semiala, si noterà che essa forma due trapezi, di cui, il maggiore si estende dalla prima alla tredicesima centina, ed il minore dalla tredicesima sino all’estremità alare.

Peso dell’ala e momento flettente

            Possedendo ora i dati relativi alla distribuzione della portanza lungo l’apertura alare, è possibile calcolare il momento flettente che essa genera ed a cui la struttura del longherone deve resistere. Prima di eseguire questo calcolo, però, è necessario determinare il punto di applicazione della forza peso dell’ala stessa, in modo da poter calcolare il momento flettente causato dal peso della struttura.

Dai dati ricavati attraverso la consultazione dei manuali di volo relativi al Bf. 109, è stato possibile determinare il peso dell’ala “Q_a”, pari a 4415N (450kg). Naturalmente, per i calcoli che si andranno ad effettuare, non si impiegherà il peso di tutta l’ala ma solo quello di una semiala “Q_sa”, pari a 2207N.

Bisogna considerare però, il fatto che il momento flettente generato dal peso dell’ala non dovrà essere considerato rispetto alla sezione di mezzeria del velivolo, ma rispetto a quella di radice del longherone. Si renderebbe necessaria, quindi, la conoscenza dell’esatta distribuzione di peso all’interno dell’ala.

A causa dell’impossibilità di determinare questo dato, si  considererà l’ala come un corpo uniforme: da questa considerazione potrà essere ricavato il peso teorico per unità di superficie della struttura alare, attraverso il quale potrà essere determinato il peso della parte di ala generante un momento flettente sopportato dalla sezione di radice del longherone. Bisogna evidenziare, comunque, che quello in uso è un metodo approssimato, ma come per quello utilizzato per la determinazione della distribuzione della portanza darà come risultato un leggero sovradimensionamento del longherone, a favore della sicurezza.

Il peso per unità di superficie dell’ala sarà, quindi:

Si determina quindi, che la superficie dell’ala compresa tra la centina n°01 e l’estremità alare è pari all’area di un trapezio avente per base maggiore la lunghezza della corda relativa alla centina 01, per base minore la corda teorica di lunghezza pari a 1.0039m, e per altezza la distanza tra la centina 01 e l’estremità alare, pari a 4.3666m. Andando ad eseguire i calcoli, si avrà:

Alla quale corrisponderà un peso di

Questo peso potrà essere considerato concentrato nel baricentro della parte di ala considerata, ed essendo questa a forma trapezia si avrà che la distanza del suo baricentro dalla centina n°01 sarà

                    [f.11]

              Prima di calcolare il momento flettente agente sulla sezione di radice del longherone, è necessario analizzare nuovamente la distribuzione della portanza lungo la semiala considerata: come è stato possibile osservare, la portanza assume un andamento trapezoidale tra le sezioni comprese tra quelle relative alle centine 01 e 13.

Attuando l’ipotesi semplificativa con la quale è stato possibile determinare l’andamento della portanza nella zona compresa tra la centina 13 e l’estremità alare, è possibile affermare che la portanza assume un andamento trapezio lungo tutta la lunghezza della semiala, e che la risultante di tutte le forze portanti esistenti lungo la semiala è data dall’area del trapezio avente come base maggiore il valore della portanza nella sezione relativa alla centina 01, come base minore il valore quello relativo alla sezione teorica situata all’estremità alare e come altezza la lunghezza della semiala considerata dal punto in cui è installata la centina 01 sino all’estremità alare.

Definita, quindi, la portanza teorica all’estremità alare

ed indicando quindi con P₁ la portanza totale agente sulla semiala, sarà possibile scrivere

                  [f.12]

Molta importanza riveste anche la determinazione del baricentro del trapezio  di portanza prima identificato, in quanto presenta il punto di applicazione nel quale è possibile considerare concentrata la P_1. Ricordando la [f.11], si determina la posizione del baricentro della portanza:

                [f.13]

Naturalmente, le formule [f.12] ed [f.13] sono approssimate, in quanto partono dall’ipotesi che l’andamento della portanza risulti essere veramente trapezoidale. Come è stato possibile notare dal grafico della distribuzione della portanza lungo la semiala, questa è quasi trapezoidale, e l’approssimazione fatta non comporta scostamenti rilevanti tra i dati teorici e quelli pratici. Volendo utilizzare un metodo matematico meno approssimato, sarebbe necessario impiegare le funzioni integrali, ottenendo le seguenti formule:

  Sarà ora possibile determinare il momento flettente agente alla radice del longherone secondo la formula:

 

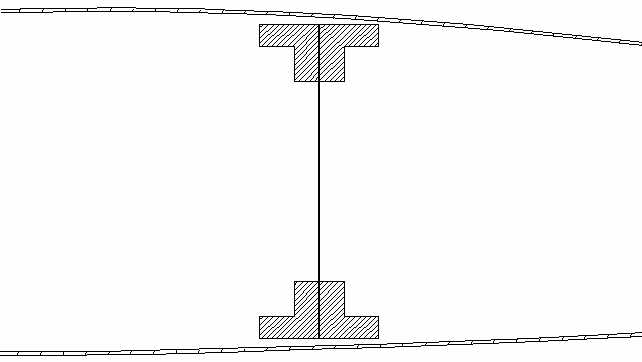
Calcolo delle dimensioni del longherone

            Il longherone è la parte strutturale dell’ala preposta a far fronte ai carichi dovuti ai momenti flettenti che si originano a causa del peso e della portanza agenti sull’ala. Ogni sezione del longherone, quindi, dovrà contrastare il momento flettente totale (cioè la somma dei momenti flettenti dovuti a portanza e peso) generato dalla parte di semiala compresa tra la sezione considerata e l’estremità alare.

Detto questo, è semplice comprendere che, più la sezione considerata si avvicina a quella relativa alla centina 01, cioè alla prima delle sezioni alari veramente portanti, e più sarà estesa la parte di semiala da considerare. Questo comporta un aumento del valore dei momenti flettenti dovuti a portanza e peso, in quanto, maggiore è la superficie alare considerata e maggiore è la portanza da essa prodotta, e maggiore sarà anche il peso dell’ala relativo a tale superficie.

            Il momento flettente Mf_rad precedentemente calcolato, quindi, sarà pari al massimo momento alare ammissibile, in quanto calcolato rispetto alla sezione di radice del longherone, cioè rispetto a quella relativa alla centina 01. In base a questo valore verrà progettato il longherone, il quale, per motivi di sicurezza, verrà opportunamente sovradimensionato attraverso un fattore di sicurezza “k”, che per questo velivolo è pari a 1.8.

            Dato il massimo momento flettente ammissibile, resta da progettare il longherone: il Bf. 109 montava un solo longherone per ogni semiala, la cui forma è assimilabile a quella di una trave con un profilo a doppio T. Le parti fondamentali di cui è costituito il longherone sono due: le solette e l’anima. L’anima è l’elemento verticale, che si estende per tutta l’altezza del longherone, ed e adibita a sopportare gli sforzi di taglio generati dai carichi agenti sull’ala. Le solette, invece, sono degli elementi posti agli estremi superiore ed inferiore del longherone, ed adibiti a far fronte ai carichi di compressione e trazione dovuti al momento causato dai carichi alari.

Seguendo le linee del progetto originale relativo alle solette, il longherone considerato verrà dotato di quattro solette dotate di profilo ad “L”, poste a due a due all’estremità superiore ed inferiore del longherone, in modo da dare a questo la forma di una trave a doppio T.

Sforzi agenti sulle solette

           

 

 

 

 

 

 

 

 

  Il momento flettente dovuto ai carichi alari che va ad agire su di una determinata sezione del longherone è dato dal prodotto di una forza per una lunghezza (detta braccio). Noto che un momento è uguale ad una coppia di forze, una volta impostata la distanza interposta tra le due forze costituenti la coppia è possibile, dividendo il momento stesso per questa distanza, ottenere l’intensità delle forze costituenti la coppia.

Nel caso specifico, una volta stabilita la distanza verticale tra i baricentri delle solette del longherone, sarà possibile, dividendo il momento flettente agente su di una determinata sezione considerata per tale distanza, ottenere gli sforzi di trazione e di compressione agenti sulle solette. Una volta determinato il materiale da utilizzare per la costruzione delle solette, sarà possibile ricavarne l’area di queste.

Calcolo delle dimensioni delle solette per la sezione di radice del longherone

            Per determinare l’entità degli sforzi di trazione e compressione agenti sulle solette del longherone nella sezione relativa alla centina 01, è necessario stabilire la distanza verticale “h_v” tra i baricentri delle solette. Per fare questo, è necessario considerare le dimensioni del profilo alare relativo a questa sezione e la forma che le solette andranno ad assumere. Dato che il longherone è posto al 40% della corda, è necessario misurare lo spessore massimo del profilo in questo punto; una volta ricavata questa misura, pari a 290mm, si rende indispensabile stabilire l’altezza massima del longherone: ipotizzando uno spessore della copertura di tre millimetri ed uno spazio necessario all’inserimento degli attacchi longherone-centina-copertura di quattro millimetri, si ricava che l’altezza massima del longherone è di 276mm.

Stabilita la forma delle solette (profilo ad “L”), indicate con “b_L” e con “s_L”  la lunghezza della base e lo spessore della soletta, con “y_GL” la distanza verticale del baricentro di una soletta calcolata dalla base della soletta stessa, con “h_long” l’altezza del longherone, pari a 276mm, con “Am” l’area minima di una soletta, con “F_fless” la forza di trazione o compressione derivante dal momento flettente (agente su entrambe le solette superiori od inferiori) e con “s” e “s_a” rispettivamente la tensione di snervamento del materiale utilizzato e la tensione massima ammissibile da utilizzare per il progetto del longherone,  è possibile scrivere le seguenti  formule:  

   [f.14]

Per determinare le dimensioni delle solette, quindi, si procederà nel seguente modo: si supponga un valore per b_L, tenendo conto che questo valore non deve essere molto elevato, in quanto, oltre ad aumentare l’area resistente della parte più esterna della soletta, fa diminuire la distanza tra i baricentri h_v, e questo porterebbe ad un aumento della F_fless agente sulle solette, con un conseguente aumento dell’aerea minima necessaria. Ipotizzando che b_L sia pari a 50mm, si fa variare il valore di s_L, in modo da determinare una condizione in cui l’area della soletta calcolata in base a b_L ed s_L (indicata con Ac) risulti uguale o leggermente maggiore di quella minima necessaria Am. L’unico dato mancante per effettuare questo calcolo risulta essere s: rispettando i parametri del progetto originale del longherone, il materiale utilizzato per la sua realizzazione risulta essere un particolare duralluminio, avente carico di snervamento pari a 451.26 N/mm² (46 kg/mm²).